数据结构“图”

图是一种非线性数据结构，由「节点（顶点）」和「边」组成，每条边连接一对顶点。根据边的方向有无，图可分为「有向图」和「无向图」。本文以无向图为例开展介绍。

如下图所示，此无向图的顶点和边集合分别为：

顶点集合： vertices = {1, 2, 3, 4, 5}
边集合： edges = {(1, 2), (1, 3), (1, 4), (1, 5), (2, 4), (3, 5), (4, 5)}

表示图的方法通常有两种：

邻接矩阵：使用数组 vertices 存储顶点，邻接矩阵 edges 存储边； edges[i][j] 代表节点 i + 1 和节点 j + 1 之间是否有边。

C++实现如下：

int vertices[5] = {1, 2, 3, 4, 5};
int edges[5][5] = {{0, 1, 1, 1, 1},
                   {1, 0, 0, 1, 0},
                   {1, 0, 0, 0, 1},
                   {1, 1, 0, 0, 1},
                   {1, 0, 1, 1, 0}};

邻接表：使用数组 vertices 存储顶点，邻接表 edges 存储边。 edges 为一个二维容器，第一维 i 代表顶点索引，第二维 edges[i] 存储此顶点对应的边集和；例如 edges[0] = [1, 2, 3, 4] 代表 vertices[0] 的边集合为 [1, 2, 3, 4] 。

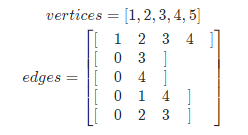
C++实现如下：

int vertices[5] = {1, 2, 3, 4, 5};
vector<vector<int>> edges;

vector<int> edge_1 = {1, 2, 3, 4};
vector<int> edge_2 = {0, 3};
vector<int> edge_3 = {0, 4};
vector<int> edge_4 = {0, 1, 4};
vector<int> edge_5 = {0, 2, 3};
edges.push_back(edge_1);
edges.push_back(edge_2);
edges.push_back(edge_3);
edges.push_back(edge_4);
edges.push_back(edge_5);

邻接矩阵 VS 邻接表：

邻接矩阵的大小只与节点数量有关，即 N^2，其中 N 为节点数量。因此，当边数量明显少于节点数量时，使用邻接矩阵存储图会造成较大的内存浪费。
因此，邻接表适合存储稀疏图（顶点较多、边较少）； 邻接矩阵适合存储稠密图（顶点较少、边较多）。